Table of Contents
Introduction
The fitting module is dedicated to the smooth fitting of point clouds and extraction of useful geometric properties. Figure 1(a) shows a typical example in 2D: we reconstruct a potential function (shown in fake colors) from a few 2D points equipped with normals; then the 0-isoline of this potential gives us an implicit curve (in orange) from which we can readily extract further properties like curvature. A great benefit of this implicit technique [6] is that it works in arbitrary dimensions: Figures 1(b-c) show how we reconstruct an implicit 3D surface with the same approach, starting from a 3D point cloud. Working with meshes then simply consists of only considering their vertices.
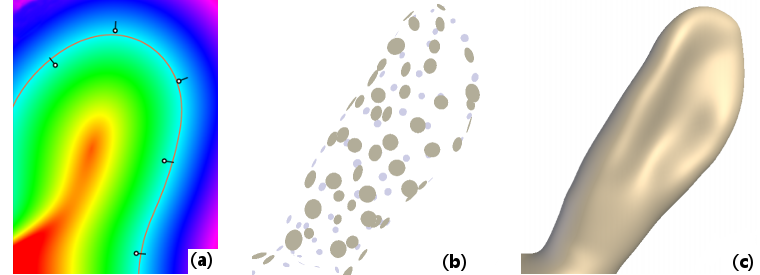
This is just the tip of the iceberg though, as we also provide methods for dealing with points equipped with non-oriented normals [4], techniques to analyze points clouds in scale-space to discover salient structures [10], methods to compute multi-scale principal curvatures [11] and methods to compute surface variation using a plane instead of a sphere for the fitting [12].
Design choices and programing techniques
The goal of this module is to provide lightweight, fast and generic algorithms for 3d point cloud processing. We mostly focus on local regression techniques, which are core components of surface reconstruction techniques [2] [6], geometric descriptors [10] [8] or shape analysis techniques [7]. Most of these techniques share similar computation, and can be combined in several ways. For instance, NormalDerivativesCurvatureEstimator estimates curvature values by analyzing the spatial derivatives of a normal field, and can be combined with any normal estimation technique.
In order to ease the association of multiple computational components, the library is based on the Curiously Recurring Template Pattern (CRTP). In contrast with polymorphism, this method allows to combine multiple short computations without adding runtime overhead (both in terms of memory footprint and execution time). Instead, the combination of the computational components is performed and optimized when compiling the program, and thus require more memory and time for this stage.
Because of some properties of the C++ language, our classes does not inherit from a Base interface defining the API, but rather follows concepts, as described in Fitting module: Concepts.
Fitting primitives and compute neighborhood properties
The fitting module provides a unified API to perform computations (e.g. fit a Primitive, compute geometrical properties such as Curvatures) over the neighborhood of a given point. The type of computation is controlled by a type (called Fit in the example below) defined by the user by combining computational components offered in this module. Given an object of type Fit, the client code will always looks as follows:
Once computations are done, the Fit object provides both getters to the neighborhood properties (e.g. estimated curvature), and procedures (e.g. projection operator onto the fitted primitive):
The Spatial Partitioning module provides data-structures to collect neighborhood in point clouds.
Fitting techniques overview
We provide various approaches to approximate, analyze or characterize the geometric properties of local neighborhoods. In most situations, all these tools are based on the estimation of a geometric Primitive approximating the neighborhood, on top of which we provide more advanced computations. The table below summarizes the Primitives available in the library, as well as the associated fitting techniques:
| Primitive | Required Input | Fitting techniques |
|---|---|---|
| Barycenter | Points only | MeanPosition (nD) |
| Normal Vector | Oriented points | MeanNormal (nD, co-dimension 1) |
| Covariance Matrix | Points only | CovarianceFitBase (nD) |
| Line | Points only | CovarianceLineFitImpl (nD) |
| Plane | Points only | CovariancePlaneFitImpl (nD) |
| Plane | Oriented points | MeanPlaneFitImpl (nD, co-dimension 1) |
| MongePatch | Points only | MongePatch (3D) |
| AlgebraicSphere | Points only | SphereFitImpl (nD) [6] |
| AlgebraicSphere | Oriented points | OrientedSphereFitImpl (nD) [6] |
| AlgebraicSphere | Non-oriented points | UnorientedSphereFitImpl (nD) [4] |
See section Computational objets, basket and CRTP for more details on how these primitives can be extended for more advanced computation.
Structure of the documentation
In the following, we focus on a basic use of the module, and detail how to:
- set up data samples that interface with an external code (see Section Data Samples),
- assemble the computational objects to define a fitting object (see Section Definition of the Fitting object)
- run the fitting process in itself (see Section Fitting Process),
- and finally collect outputs (see Section Basic Outputs).
We also show detail all the available tools for geometrical property estimation (see Section Computational objets, basket and CRTP), with a specific focus on curvature (see Section Computing Curvatures). The last section details how to use this module on CUDA kernels (see Section Cuda).
First Steps
Include directives
The Fitting module defines operators that rely on no data structure and work both with CUDA and C++. These core operators implement atomic scientific contributions that are agnostic of the host application. If you want to use the Fitting module, just include its header:
Data Samples
The first step needed to use Ponca is to define how samples are represented inside the module. A strength of Ponca is to define all these structures at compile time to generate optimized code for fast evaluation at runtime.
The class Ponca::Concept::PointConcept defines the interface that has to be implemented to represent a sample. Observe that there is no need for data conversion: all you need to do is to indicate how to access existing data (see the example Ponca data-structure binding).
As an example, let's fit a AlgebraicSphere onto points equipped with normals using Ponca::OrientedSphereFit. To this end, we must define a structure (denoted PointPositionNormal in the example below) containing a normal vector and its associated accessors. Depending on the fitting procedure we will use, we may need to define a MatrixType type. This is for instance required for Computing Curvatures. This leads to the following class:
- Note
- The macro
PONCA_MULTIARCHis optional and required only for Cuda support.
PointPositionNormal needs to be specialized for any scalar type or dimension (you may also use a non-template class directly):
Definition of the Fitting object
Two template classes must be specialized to configure computations.
- The first step consists in specifying a weighting function: it defines how neighbor samples will contribute to the fit, as illustrated in Figure 2(a) in 2D. In this example, we choose a weight based on the Euclidean distance using Ponca::DistWeightFunc, remapped through a bisquare kernel defined in Ponca::SmoothWeightKernel: using WeightFunc = DistWeightFunc<Point, SmoothWeightKernel<Scalar> >;
- The second step identifies a complete fitting procedure through the specialization of a Ponca::Basket. In our example, we want to apply an Ponca::OrientedSphereFit to input data points, which outputs an Ponca::AlgebraicSphere by default. This leads to the following specialization: using Sphere = Basket<Point, WeightFunc, OrientedSphereFit>;
Fitting Process
At this point, most of the hard job has already been performed. All we have to do now is to provide an instance of the weight function, where \(t\) refers to the neighborhood size, and initiate the fit at an arbitrary position \(\mathbf{p}\).
Then neighbors are added sequentially: in this example, we traverse a simple array, and samples outside of the neighborhood are automatically ignored by the weighting function. Once all neighbors have been incorporated, the fit is performed and results stored in the specialized Basket object. STL-like iterators can be used directly for the fit by calling
Spatial structures can be used to accelerate spatial queries. Consider for instance using the KdTree class with range queries:
- Note
- Currently, users need to ensure consistency between the query and the fit location/scale. This is expected to be fixed in the upcoming releases.
In these examples, fit1, fit2 and fit3 should perform exactly the same computations, as long a the neighborhood remains the same between the three calls.
Check fitting status
After calling finalize or compute, it is recommended to test the return state of the Fit object before using it:
Some methods require multiple fitting passes, e.g. MongePatch. This is directly handled by the compute method. If you don't use it, you need to check if eResults == NEED_ANOTHER_PASS and repeat the addNeighbor()/finalize() steps. Don't forget to call startNewPass() at each iteration.
- Warning
- You should avoid data of low magnitude (i.e., 1 should be a significant value) to get good results; thus rescaling might be necessary.
Basic Outputs
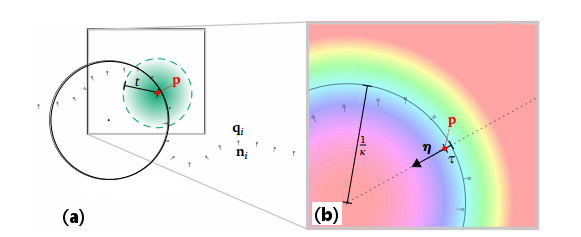
Now that you have performed fitting, you may use its outputs in a number of ways (see Figure 2(b) for an illustration in 2D).
You may directly access generic properties of the fitted Primitive:
This generates the following output:
You may rather access properties of the fitted sphere (the 0-isosurface of the fitted scalar field), as defined in AlgebraicSphere :
You will obtain:
Advanced usage
Computing derivatives
Starting from v1.0, Ponca provides BasketDiff, a class to extend an existing Basket with differentiation tools. Given a specialized type TestPlane that performs covariance plane fitting (using Ponca::CovariancePlaneFit), and defined as follows:
BasketDiff allows to extend this type to compute its derivatives in space and/or scale:
Computational objets, basket and CRTP
In addition to Primitive fitting, Ponca allows to compute geometrical properties of the input samples. This is done by aggregating multiple tool classes in the Basket, for instance to compute the Growing Least Squares descriptor [10] (see GLSParam) from multiple sphere fitting techniques:
From a technical point of view, the Basket class combines its template parameters (here Ponca::OrientedSphereFit and GLSParam) following the CRTP rules, ie. to form an object of the type GLSParam<Ponca::OrientedSphereFit<DataPoint, _WFunctor,T>>, that aggregates the computations provided in each class of the hierarchy.
In practice, Ponca uses these mechanisms under the hood in order to combine atomic computations and minimize code duplication. For instance, Ponca::OrientedSphereFit is defined as an assembly of several computations classes:
Here, the class MeanPosition computes the mean position of the input points. It is also used in Ponca::CovariancePlaneFit:
and Ponca::MeanPlaneFit, among others.
Computational objets capabilities and requirements
Aggregating small computational objects allows to minimize code duplication, but also to easily combine different techniques. For instance, GLSDer can be used independently of the fitting technique, e.g. Ponca::OrientedSphereFit or Ponca::UnorientedSphereFit, as long as the fitted Primitive is an AlgebraicSphere.
In order to detect if the computational objects are correctly combined, Ponca provides a compile-time equirement/capability system: each computational objects check if the other classes of the CRTP provides the required computations. For instance, in the GLSParam class, we define the following enum:
Base is a type defined from the CRTP and that represents the inherited classes. If Base does not define PROVIDES_ALGEBRAIC_SPHERE, this line generates an error when compiling the program. For instance, compiling the type
generates the following error:
The capability PROVIDES_GLS_PARAMETRIZATION tells that GLSParam provides the GLS parameterization [10], and other components can access the related information.
- Note
- There is currently no formal description of the API provided by each capability. This will be fixed in upcoming releases. These relations are currently implicitly defined (and used), but not documented. For instance, a tool with the capability
PROVIDES_PRINCIPAL_CURVATURESprovides the following methods:kmin(),kmax(),kminDirection(),kmaxDirection(),kMean(),GaussianCurvature(), see CurvatureEstimatorBase.
In order to ease tools combinations, each class declare a set of required and provided capabilities, as listed in the two following table:
| Fit/Tool (used in Basket) | Requires | Provides |
|---|---|---|
| MeanPosition | PROVIDES_MEAN_POSITION | |
| MeanNormal | PROVIDES_MEAN_NORMAL | |
| PrimitiveBase | PROVIDES_PRIMITIVE_BASE | |
| DryFit | PROVIDES_PRIMITIVE_BASE | |
| Plane | PROVIDES_PRIMITIVE_BASE | PROVIDES_PLANE |
| Ponca::MeanPlaneFitImpl | PROVIDES_MEAN_POSITION,PROVIDES_MEAN_NORMAL,PROVIDES_PLANE | |
| CovarianceFitBase | PROVIDES_MEAN_POSITION | PROVIDES_POSITION_COVARIANCE |
| Ponca::CovarianceLineFitImpl | PROVIDES_LINE,PROVIDES_POSITION_COVARIANCE | |
| Ponca::CovariancePlaneFitImpl | PROVIDES_PLANE,PROVIDES_POSITION_COVARIANCE | PROVIDES_TANGENT_PLANE_BASIS |
| MongePatch | PROVIDES_TANGENT_PLANE_BASIS,PROVIDES_PLANE | |
| AlgebraicSphere | PROVIDES_PRIMITIVE_BASE | PROVIDES_ALGEBRAIC_SPHERE |
| Ponca::SphereFitImpl | PROVIDES_ALGEBRAIC_SPHERE | |
| Ponca::OrientedSphereFitImpl | PROVIDES_ALGEBRAIC_SPHERE,PROVIDES_MEAN_NORMAL,PROVIDES_MEAN_POSITION | |
| Ponca::UnorientedSphereFitImpl | PROVIDES_ALGEBRAIC_SPHERE,PROVIDES_MEAN_POSITION | |
| GLSParam | PROVIDES_ALGEBRAIC_SPHERE | PROVIDES_GLS_PARAMETRIZATION |
| Fit/Tool (used in BasketDiff) | Requires | Provides |
|---|---|---|
| PrimitiveDer | PROVIDES_PRIMITIVE_BASE | PROVIDES_PRIMITIVE_DERIVATIVE |
| CovarianceFitDer | PROVIDES_PRIMITIVE_DERIVATIVE,PROVIDES_MEAN_POSITION_DERIVATIVE,PROVIDES_POSITION_COVARIANCE | PROVIDES_POSITION_COVARIANCE_DERIVATIVE |
| Ponca::CovariancePlaneDerImpl | PROVIDES_PLANE,PROVIDES_POSITION_COVARIANCE_DERIVATIVE | PROVIDES_COVARIANCE_PLANE_DERIVATIVE,PROVIDES_NORMAL_DERIVATIVE |
| Ponca::OrientedSphereDerImpl | PROVIDES_ALGEBRAIC_SPHERE,PROVIDES_MEAN_POSITION_DERIVATIVE,PROVIDES_PRIMITIVE_DERIVATIVE | PROVIDES_ALGEBRAIC_SPHERE_DERIVATIVE,PROVIDES_NORMAL_DERIVATIVE |
| MlsSphereFitDer | PROVIDES_PRIMITIVE_DERIVATIVE,PROVIDES_ALGEBRAIC_SPHERE_DERIVATIVE | PROVIDES_NORMAL_DERIVATIVE |
| GLSDer | PROVIDES_GLS_PARAMETRIZATION,PROVIDES_PRIMITIVE_DERIVATIVE,PROVIDES_ALGEBRAIC_SPHERE_DERIVATIVE | PROVIDES_GLS_DERIVATIVE,PROVIDES_GLS_GEOM_VAR |
| CurvatureEstimatorBase | PROVIDES_PRINCIPAL_CURVATURES | |
| NormalDerivativesCurvatureEstimator | PROVIDES_NORMAL_DERIVATIVE,PROVIDES_PRINCIPAL_CURVATURES | |
| NormalCovarianceCurvatureEstimator | PROVIDES_PRINCIPAL_CURVATURES | |
| ProjectedNormalCovarianceCurvatureEstimator | PROVIDES_PLANE |
- Note
- In its current version, the requirement/capability system offer limited protection over the combination of tools providing the same capabilities. Indeed, it is possible to build ill-formed combinations where two computations attempt to save their results at the same place, e.g. when using two fitting technique for the same primitive: This case is not detected at compile time, but rather dynamically when calling finalize(), which can now return CONFLICT_ERROR_FOUND. Internally, this is implemented by checking if the primitive is already valid (ie. it has been computed already) when finalizing the computation. This limitation is expected to be resolved in upcoming releases.typedef Basket<Point, WeightConstantFunc, Plane,MeanNormal, MeanPosition, MeanPlaneFitImpl,CovarianceFitBase, CovariancePlaneFitImpl> Hybrid1; //test conflict detection in one direction
Sharing computations between fits
In most cases, only one primitive is included in the Basket, and it is recommended to use the helper classes provided by Ponca for fitting, e.g. Ponca::CovariancePlaneFitImpl, Ponca::OrientedSphereFitImpl. Starting from version 1.0.0, Ponca allows to combine multiple primitives. In order to share intermediate computation results, it is recommended to explicitly define the computational arrangement, e.g.:
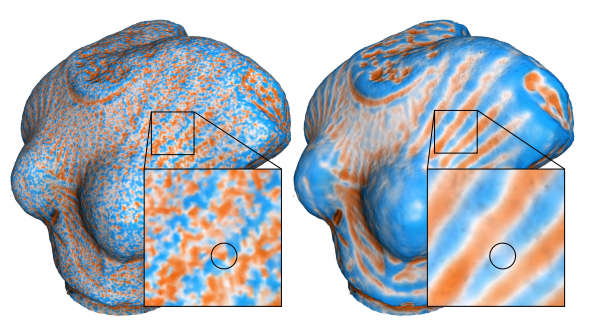
Computing Curvatures
Ponca offers several ways to compute curvatures, some of which are reviewed and compared by Lejemble et al. in [8] and listed in the table below:
| Estimator Name | Estimated quantities | Usage | Speed | Robustness |
|---|---|---|---|---|
| Distance to PCA plane [5] | Mean curvature | Basket<P,W,CovariancePlaneFit> // method potential() | +++ | - |
| Surface Variation [12] | Mean curvature | Basket<P,W,CovariancePlaneFit> // method surfaceVariation() | +++ | - |
| Growing Least Squares [10] | Mean curvature | Basket<P,W,OrientedSphereFit,GLSParam> // method kappa() | ++ | + + |
| Point Set Surfaces (PSS) [2] | Curvature Tensor | Basket<P,W,CovariancePlaneFit,CovariancePlaneSpaceDer,NormalDerivativesCurvatureEstimator> | +++ | + |
| Algebraic Point Set Surfaces (APSS) [6] | Curvature Tensor | Basket<P,W,OrientedSphereFit,OrientedSphereSpaceDer,NormalDerivativesCurvatureEstimator> | ++ | + + |
| Algebraic Shape Operator (ASO) [8] | Curvature Tensor | Basket<P,W,OrientedSphereFit,OrientedSphereSpaceDer,MlsSphereFitDer,NormalDerivativesCurvatureEstimator> | + | + + + |
Cuda
Ponca can be used directly on GPU, thanks to several mechanisms:
- Eigen Cuda capabilities, see Eigen documentation for more details. You need to use a consistent
Eigen::Indexon both CPU and GPU if you plan to transfer memory between the computing units. That's why we recommend to set the following preprocessor variable when compiling your project:You might also need to define the-DEIGEN_DEFAULT_DENSE_INDEX_TYPE=int--expt-relaxed-constexprpreprocessor option forNVCC. Example of working cmake file (see Screen Space Curvature using Cuda/C++):enable_language(CUDA)add_executable(ponca_ssgls "ponca_ssgls.cu")target_compile_options(ponca_ssgls PRIVATE --expt-relaxed-constexpr) - Automatic CPU/GPU compilation qualifiers. We use the macro to use the same code for C++ and CUDA. It has no effect when the code is compiled with GCC or Clang, but it will force the compilation for both host and device architectures when compiling with nvcc. A similar macro system is provided for mathematical functions, to switch between STL and CUDA versions.PONCA_MULTIARCH void function();
Check the C++/Cuda and Python/Cuda (using PyCuda) examples for more details and how-to.
